감쇠 예제 (attenuation exmple)

 

 

예를 들어, 지름이 60.96cm(24인치)이고 벽이 1.27cm(0.5인치)인 강관을 고려해봅시다. 강관의 전기 저항율이 13.4 µohm-cm(5.29 µohm-in.)이라고 가정합니다. 강관 외경의 단면적 A는 238.15cm²(36.91in²)입니다. 단위 길이 L을 16.09km(10.0마일)로 선택하면 강관의 단위 길이당 선형 저항은 다음과 같습니다:

 

누설 전도도 g는 코팅의 종류, 토양의 전기 저항율 및 코팅 결함의 수와 크기에 따라 달라집니다. 강관의 저항과 달리 누설 전도도는 정확하게 결정할 수 없으며 경험에 기초하거나 구조물 완성 후 실제 테스트로 추정할 수 있습니다. Table 2.6에는 1,000 Ω-cm 토양에서의 특정 누설 전도도 g'의 몇 가지 전형적인 값이 나와 있습니다. 우수한 품질의 코팅이며 주요 결함(Holiydays)이 없다면 1000 Ω-cm 토양에서의 특정 누설 전도도를 4.3 x 10^-5 S/m²로 가정할 수 있습니다. 이는 강관의 단위 길이당 평균 특정 파이프-원격 지구 저항이 23255 Ω-m² (250,348 Ω -ft²)임을 의미합니다. 배관의 단위 길이당 표면적은 다음과 같습니다:

만약 평균 토양 전기 저항율이 5,000 Ω-cm 인 경우, 누설 전도도는 비례적으로 감소할 것입니다:

이로 인해 5,000 Ω-cm 토양에서의 전파 감쇠 상수는 다음과 같습니다:

그리고 강관의 특성 저항은 다음과 같습니다:

전파 상수와 특성 저항을 계산한 후 디자이너는 Figure 2.17의 일반 방정식을 사용하여 파이프라인에 배치된 모든 전원 소스에 대한 전류 분포 및 파이프-지속 전압 이동을 계산할 수 있습니다.

위의 상수를 가진 파이프라인이 양 끝에서 전기적으로 격리된 10 단위 길이라고 가정해 봅시다. 디자인 엔지니어는 라인의 한쪽 끝에 적용된 전기방식 전원으로 인한 영향을 알고 싶어합니다.

Figure 2.18, Equation 5에서 수신측에서 x 단위 떨어진 소스 쪽에서 파이프라인과 원격 지구 간의 저항을 계산합니다.

오옴의 법칙에 따르면 소스에서 되돌아온 1.0A는 배관의 전위를 원격 지구(Remote Earth)의 전위로 이동(shift)시킵니다:

 

이제 Figure 2.18, Equation 3을 사용하여 소스에서 10 단위만큼 떨어진 수신측에서 전압 이동을 계산합니다.

 

수신측에서의 전위 이동은 소스 쪽의 약 41% 정도입니다.

 

Figure 2.18의 방정식을 사용하여 파이프라인의 모든 지점에서 소스 전류의 백분율 및 라인을 따라 받는 차등 전류를 계산할 수 있습니다.

전기적 Long 모델

"전기적으로 Long" 것은 이전 단락에서 언급한 대로, 긴 파이프 라인과 지하전극 헤더 케이블은 직류 전기 전송선으로 모델링할 수 있습니다. 입력 변수인 전류와 전압의 크기는 감쇄 상수에 의해 결정되어 입력 라인의 입력부터 거리가 증가함에 따라 감소하거나 감쇄됩니다. 만약 라인이 물리적으로 충분히 길거나 감쇄 상수가 충분히 크다면 입력 변수는 어느 정도 거리에서는 제로에 가까워질 것입니다. 전송 시스템이 입력 변수가 제로에 가까워지는 상황이라면 그 라인을 "전기적으로 긴 것"이라고 합니다.

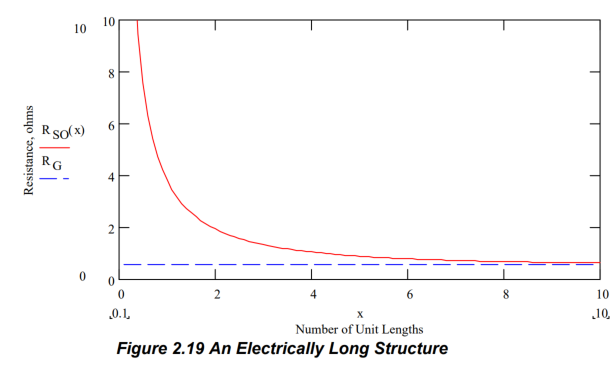
전기적으로 긴 전송 라인은 입력 변수가 라인의 수신 끝에서 감지될 수 없는 전송 라인으로 정의됩니다. 또 다른 전기적으로 긴 것을 정의하는 방법은 입력 저항이 해당 특성 저항과 동일한 전송 라인이라고 하는 것입니다. 다시 말해, 주어진 전송 라인의 길이가 증가함에 따라 입력 저항이 감소하다가 특성 저항에 도달합니다. 특성 저항에 도달하면 추가적인 라인 길이가 입력 저항에 영향을 미치지 않습니다. 이 길이에서 입력 변수는 라인의 수신 끝에서 감지될 수 없게 됩니다. 이것은 이전 전송 라인 예시에 대한 입력 저항(RSO) 대 라인 길이의 그래프에서 확인할 수 있습니다.

 

다시 자세히 설명하면

 

전기적으로 긴 파이프라인 및 지중 헤더 케이블은 이전 단락에서 언급한 대로 DC 전기 전송 라인으로 모델링될 수 있습니다. 입력 변수인 전류 및 전압의 크기는 전송 라인의 입력 끝에서 거리가 증가함에 따라 감쇠하며, 이는 감쇠 상수에 의해 결정됩니다. 라인이 물리적으로 충분히 길거나 감쇠 상수가 충분히 크면 입력 변수는 어느 정도의 거리에서는 zeor에 가까워질 것입니다. 전송 시스템이 입력 변수가 zero에 가까워지면 해당 라인은 "전기적으로 긴"이라고합니다.

 

전기적으로 긴 전송 라인은 입력 변수를 라인의 수신 끝에서 감지할 수 없는 전송 라인으로 정의됩니다. 또 다른 방법으로 전기적으로 긴이라는 것은 입력 저항이 특성 저항과 동일한 전송 라인입니다. 다시 말해 특정 전송 라인의 길이가 증가함에 따라 입력 저항이 감소하여 특성 저항에 도달할 때까지입니다. 특성 저항에 도달하면 추가 라인 길이가 입력 저항에 영향을 미치지 않습니다. 이 길이에서 입력 변수는 라인의 수신 끝에서 감지할 수 없습니다. 이는 이전 전송 라인 예제에 대한 입력 저항(R_SO) 대 길이의 플롯에서 확인할 수 있습니다. Figure 2.19를 참조하십시오.

 

종합하면, 입력 저항은 특성 저항과 일치하게 됩니다. Figure 2.19를 참조하세요.

 

전기적으로 긴 전송 라인을 정의하는 다른 방법은 입력 저항이 특성 저항과 동일한 라인입니다. 특성 저항에 도달하면 라인은 더 이상 입력 변수를 수신 끝에서 감지하지 않게 됩니다. Figure 2.19에서 확인할 수 있듯이 입력 저항이 특성 저항에 도달하면 추가 라인 길이가 입력 저항에 미치는 영향이 줄어듭니다.

전기적으로 긴 라인에서는 입력 변수의 크기가 라인의 길이와 함께 증가함에 따라 점차적으로 작아지게 됩니다. 라인이 전기적으로 길면 입력 변수가 일부 거리에서는 감지되지 않게 되며, 이를 "전기적으로 Long"이라고 합니다.

Figure 2.19에서 알 수 있듯이, 입력 저항(R_SO)이 특성 저항과 일치하는 지점에서 더 이상 길이의 증가가 입력 저항에 미치는 영향이 없게 됩니다. 이 길이에서 입력 변수는 수신 끝에서 감지할 수 없게 됩니다.

Figure 2.19의 플롯은 특정 라인 길이에서 입력 저항이 특성 저항과 동일해지면서 전기적으로 긴 라인의 개념을 시각적으로 보여줍니다.

Figure 2.19에서 보듯이, 특성 저항과 일치하는 지점에서 라인 길이의 증가가 입력 저항에 미치는 영향이 없어집니다. 이 길이에서부터 입력 변수는 수신 끝에서 감지할 수 없게 됩니다.

전기적으로 긴 라인에서는 입력 변수의 크기가 라인의 길이와 함께 감소하게 됩니다. 라인이 전기적으로 길면 입력 변수가 일부 거리에서는 더 이상 감지되지 않게 되며, 이를 "전기적으로 Long"이라고 합니다.

라인이 전기적으로 길 경우, 입력 변수의 크기가 더 이상 감지되지 않는 지점을 "전기적으로 긴"이라고 정의합니다. 또 다른 정의는 입력 저항이 특성 저항과 동일한 라인이라고 할 수 있습니다. 즉, 라인의 길이가 증가함에 따라 입력 저항이 감소하여 특성 저항에 도달하게 되면 입력 변수가 수신 끝에서 더 이상 감지되지 않게 됩니다.

Figure 2.19의 플롯은 전기적으로 긴 라인에서의 입력 저항과 길이 간의 관계를 시각적으로 보여주고 있습니다.

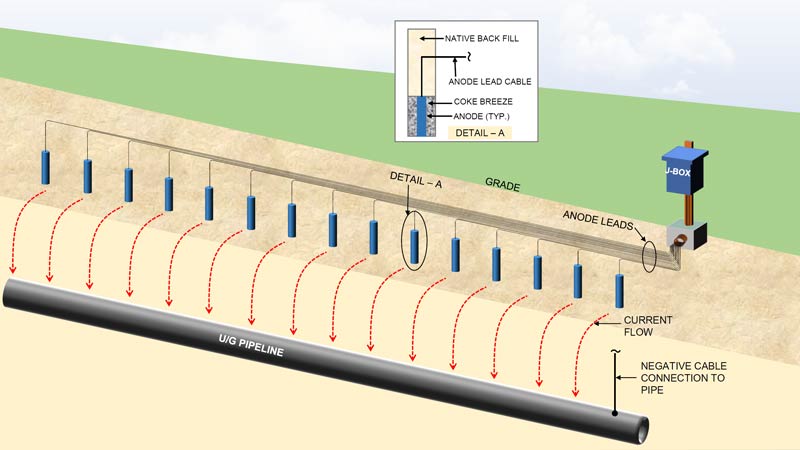
전기적으로 긴 전송 시스템이 되는 효과의 실제적인 예로서 매우 긴 헤더 케이블이 분산된 아노드에 전원을 공급하는 상황을 고려해 봅시다. 헤더 케이블의 길이가 전기적으로 길어질수록 헤더 케이블 끝에 추가 아노드를 추가해도 지구 저항에는 영향이 없을 것입니다. 또한, 정류기에서 출력 전류는 헤더 케이블을 따라 거리에 따라 감소하여 마지막 아노드에서는 전류가 방출되지 않을 것입니다. 즉 전기적으로 Long인 시스템에서는 추가적인 양극을 설치해도 일부양극에서만 전류가 발생하고 나머지에서는 전류가 발생하지 않은다.